
第六章作业思路分享

0 写在前面
状态空间法的意义
对于一个含有储能元件的网络而言,已有的研究方法是:列写多个微分方程并通过KVL和KCL,最终推导出一个高阶微分方程,再进行求解。
对高阶微分方程的求解,通常有两种途径:
- 利用高等数学求解高阶微分方程的方法,确定网络的时域解;
- 利用拉普拉斯变换的方法,把高阶微分方程变换成线性方程,待求得具体的频域解后,再利用拉式反变换求解出时域解。
本质上,两种方法只是对高阶微分方程的求解;在每次求解过程中,只能解出一个变量的时域解。其他变量的时域解,需要再列写同等阶数的高阶微分方程,才能求得。
基于高阶微分方程法的缺陷,结合《矩阵分析》的有关知识,提出了状态空间法。状态空间法将我们关心的物理量(中的几乎全部)取作状态变量中的元素。此后,基于系统中各组分间的物理约束(对于电路而言就是KVL和KCL)列出状态方程;最终,通过求解矩阵指数函数就能够将电路的零输入响应的时域解表达出来。
了解更多:
1 前置知识
- 独立储能元件与网络复杂度阶数
- 状态方程的一般形式
- 化无穷矩阵级数为有穷矩阵级数的方法
点击查看更多
对于一个含储能元件的电路而言,根据储能元件数目与独立储能元件数目是否相等,电路可分成:
- 常态网络(储能元件数 = 独立储能元件数目)
- 非常态网络
判断储能元件是否独立需要依托:
- 纯电感割集
- 纯电容回路
另外,还需要一点《线性代数》的知识。
如下图所示,左侧为纯电容回路,右侧为纯电感割集。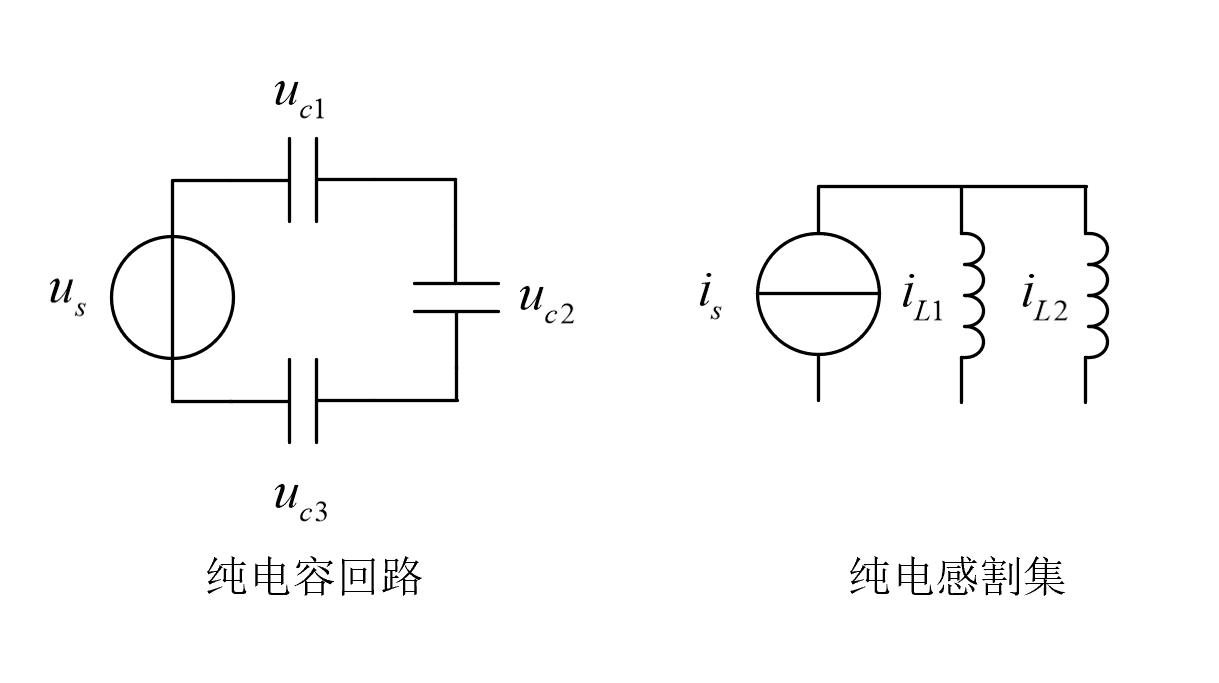
在纯电容回路和纯电感割集中,显然有: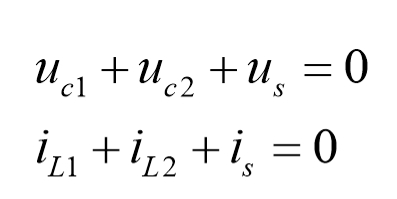
显然,若确定方程中两个未知量为基底,另外一个未知量可以被线性表示。换句话说:该方程相当于是两个n维向量的内积;一个是未知数向量,一个是数值向量。数值向量的秩是1,未知数向量的维数应当是n-1维(对应到这里就是2维)。
通过以上的说明,复现出一个问题:增加一个纯电容回路或纯电感割集,就会相应地“剥夺”一个储能元件独立储能元件的地位;该储能元件的电源或电流就能够由外电路唯一确定。
由此,我们说明完了独立储能元件的概念
1.1.2 网络复杂度阶数
网络复杂度阶数描述的是一个网络中独立储能元件的数目,显然,网络复杂度阶数=储能元件数目-纯电容回路数-纯电感割集数。
统计纯电容回路数的方法:
- 将网络中非电压源、电容的其他元件全部开路
- 统计剩下的基本回路数(对于平面网络,基本回路数就是网孔数)
统计纯电感割集的方法是类似的,即:
- 将非电感和电流源的其他元件短路
- 统计剩下的基本割集数
1.2 状态方程的一般形式
如图为状态方程的一般形式: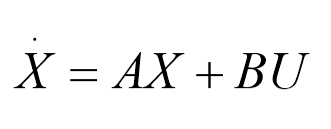
其中,x表示状态变量;x(是列向量)其中元素的数目等于网络复杂度阶数。u表示输入向量;在电网络中,输入向量数目等于网络中电源的数目。
特别地,对于非常态网络,其状态方程表达如下: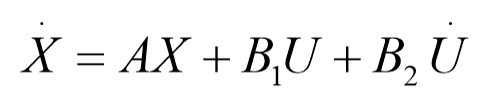
1.3 化无穷矩阵级数为有穷矩阵级数的方法
1.3.1 由矩阵的最小多项式所确定的基
对于任何一个矩阵,均可以求得其最小多项式:
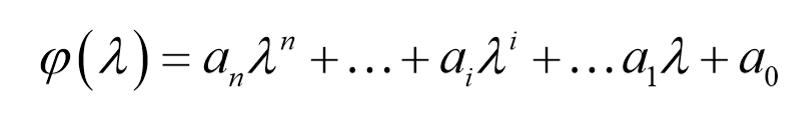
根据凯莱-哈密尔顿定理:
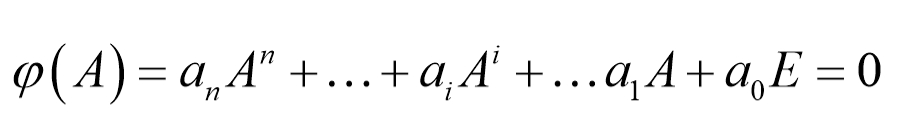
(特别地,该矩阵的特征多项式也满足上述方程。)
由此,可以找到一组基表示任意n阶及以上阶数的矩阵,且表示式的系数唯一;为了说明方便,这里取基为: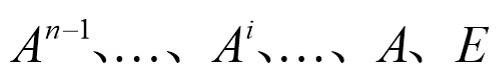
1.3.2 无穷矩阵级数的退化
对于一个可以展开成无穷级数的矩阵函数,以麦克劳林公式为例: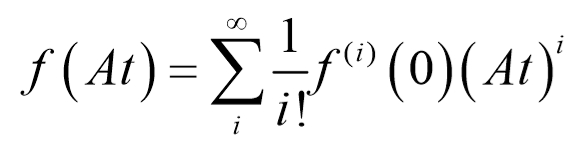
通过1.3.1中确定的一组基: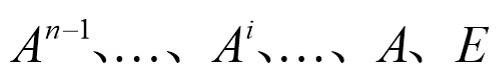
麦克劳林公式随即由无穷级数退化为有穷级数,不妨记为: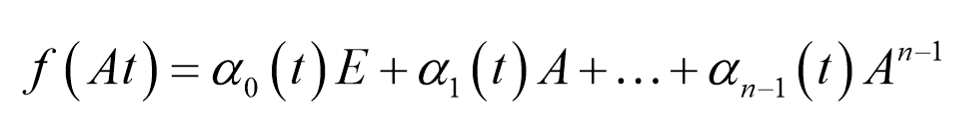
自此,我们实现了化无穷矩阵级数为有穷矩阵级数。现在的问题仅限于如何求解表达式的系数了。
1.3.3 有穷级数系数的确定
根据凯莱-哈密尔顿定理,将矩阵的特征值带入有穷级数;也满足该方程。
显然有: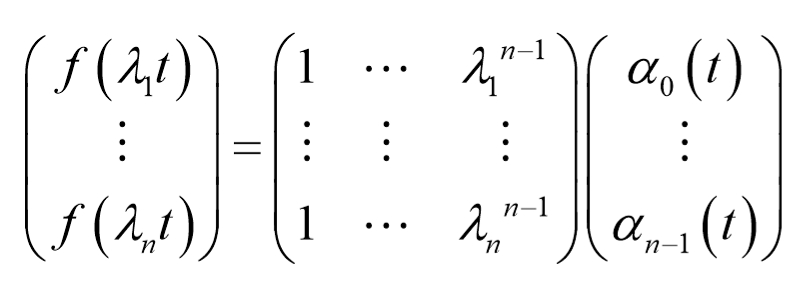
由此,我们将表示式的系数唯一确定了。
这里实际上只给出了矩阵特征值无重根的情形。
对于矩阵特征值出现重根的情况,我们应当将下式子,对特征值求导生成一个新的方程。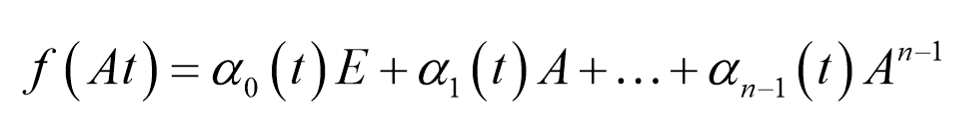
2 解题思路
2.1 列写状态方程的基本步骤
2.1.1 确定网络复杂度阶数
确定网络复杂度阶数的目的是为了确定状态变量x中元素的数目。状态变量中x的元素就能够因此而确定。
正如前文所述,网络复杂度阶数表征了状态空间中元素的数目。
一般地,对于常态网络而言,网络复杂度阶数就是储能元件数目;因此,把全部电容电压和电感电流取为状态变量中的元素就完成了状态变量的取定。
特殊地,对于非常态网络而言,网络复杂度阶数小于储能元件数目;因此,总有一些电容电压或电感电流是不能取为状态变量中的元素的。此种情况下,应根据纯电容回路和纯电感割集确定究竟是哪些电容电压和电感电流具备成为状态变量中元素的“资格”。正如1.1.1 独立储能元件的概念所阐明的那样,只有独立储能元件才能够成为网络中的状态变量。
2.1.2 确定网络的规范树
所谓规范树,其本质上就是一个树。树的概念在第二章图论的相关理论中被提出;指的是连接全部节点的不构成封闭图的最大的支路集合。
规范,是我们所要选取的这个树的定语,也暗示着取树的规则。在列写状态方程的过程中,取定树支的优先级是:
- 电压源
- 电容
- 电阻
- 电感
- 电流源
此外,还应注意:
- 状态变量中所取定的电容,必须作为树支;
- 状态变量中所取定的电感,必须作为连支。
由此,基于以上原则,我们取定了网络的规范树。
2.1.3 做规范树的基本割集和基本回路并列写方程
割集,本质上就是一个广义的节点;电容的电压作为状态变量,其电流应满足基本割集电流方程;类似地,电感所在支路的电感电压应满足基本回路的电压方程。
通过列写电容树支的基本割集电流方程、电感所在连支的基本回路电压方程,从形式上,该方程组已经基本具备了状态方程的雏形;已经是导数与变量的线性方程组。
对于常态网络,第三步的工作已经基本完成,可以进入到第四步的工作中;但对于非常态网络,我们需要补充方程,将非独立储能元件的电压或电流的导数用独立储能元件的电压或电流的导数、输入变量的电压或电流的倒数线性表示出来。
至此,我们推导出了“准状态方程”。
2.1.4 消去方程中的中间变量
状态方程最终是状态变量的导数被状态变量与输入变量(及其导数)线性表示的形式;在上一步骤中,“准状态方程”中非状态变量、输入变量(及其导数)的中间变量。为了将“准状态方程”升级为状态方程,我们需要利用网络的KCL、KVL以及电阻的VCR(欧姆定律)将中间变量消去。
2.1.5 整理
将状态方程整理成矩阵形式
2.2 用待定系数法确定矩阵指数函数
在前置知识中,我们说明了化无穷矩阵级数为有穷矩阵级数的方法;实际上,对于矩阵指数函数,其本身也可以写成无穷级数的形式。利用前置知识中的内容,我们就能够确定出矩阵指数函数。
- 标题: 第六章作业思路分享
- 作者: JinYu
- 创建于 : 2023-10-18 09:15:12
- 更新于 : 2023-10-18 14:13:03
- 链接: https://redefine.ohevan.com/2023/10/18/第六章作业思路分享/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。