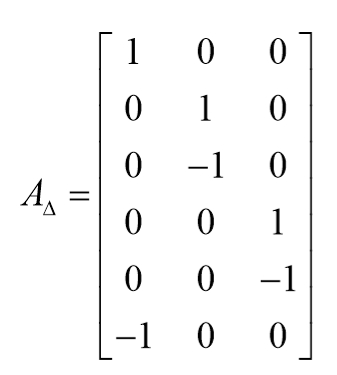第五章作业思路分享

1 前置知识
- 分裂法与网路变动
- 补偿定理
分裂法与网络变动
对于由几个简单网络通过几条简单支路连接成的一个复杂网络,实际上,节点阻抗矩阵(按网络分块后)除主对角线元素以外,在非主对角线上还存在几个元素。
这几个元素数目并不多却使得矩阵求逆的工程量变得相对较大。
如果应用网路变动的思想(主要是补偿定理),将待求的网络理解成几个简单网络增加了几条支路;并应用补偿定理,就能够将一个相对复杂高阶矩阵的求逆运算,转变成几个低阶相对简单矩阵的求逆运算过程,简化了求解运算的复杂程度。
补偿定理: 点击查看更多
这里实际上并不要求掌握
已知矩阵方程如下,要求X
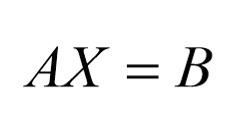
对于矩阵A
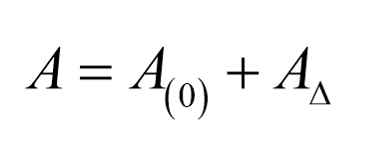
由此矩阵方程可变为:
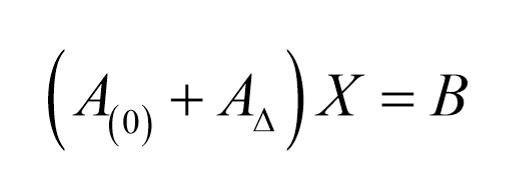
其中A矩阵的变化量可分解为
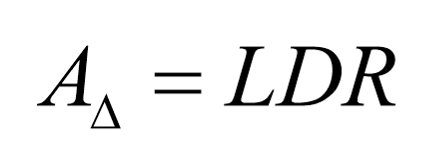
则有
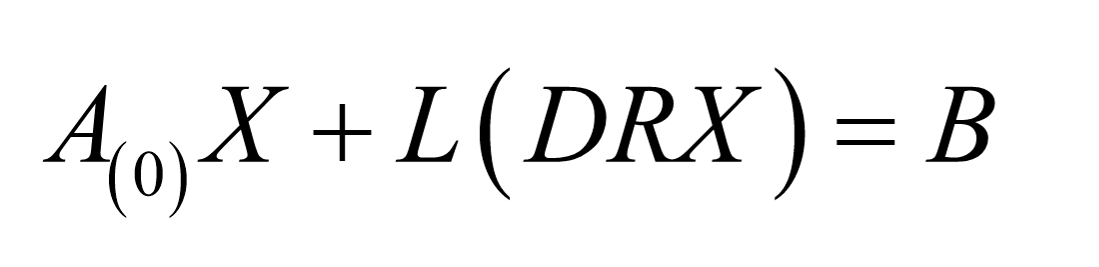
令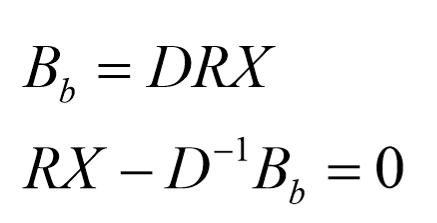
则有
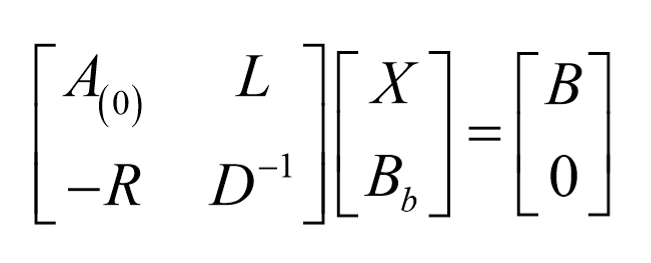
此后求解X的过程,就可以应用高斯消去法(对矩阵进行初等行变换变行阶梯,进而化成行最简)求解X
通过补偿定理的知识,分裂法可用如下矩阵进行数学描述
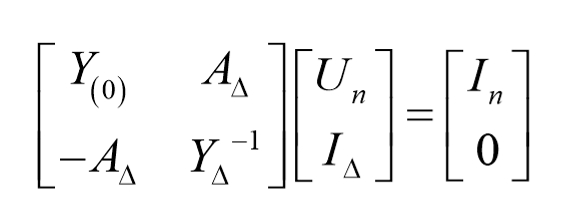
2 解题思路
生成Yn(0)
实际上,按网络分块后,Yn0中每一个子块都是相同的二阶矩阵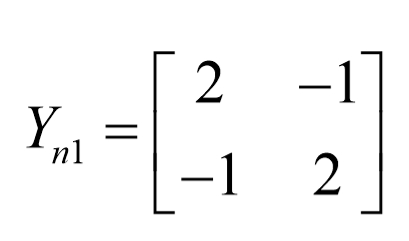
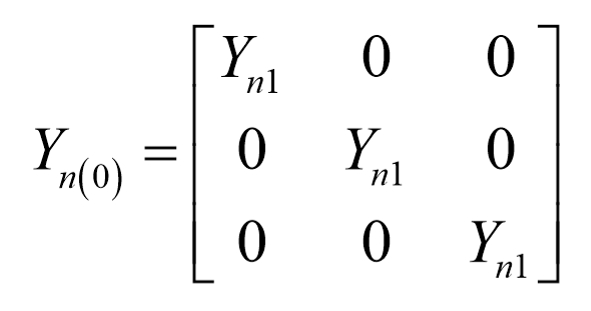
生成A阵
高斯消去
- 通过将待求矩阵化成行阶梯型,先求解支路电流
- 将支路电流带入,最终求得各节点电压
附加说明
分裂法不仅只有分裂支路电流的情况,回路电流、割集的相关参数都可以予以分裂。
从手算角度,也许分裂法过于繁琐;但从工程实际角度分析,通过繁琐的步骤,能够减小一次计算的存储容量;在一定算力的情况下,给分析大型网络提供了可能。
3 程序
为了验证手算结果的准确性,笔者基于Matlab编写了程序用以验证。
- 标题: 第五章作业思路分享
- 作者: JinYu
- 创建于 : 2023-09-20 08:18:48
- 更新于 : 2023-10-18 10:25:48
- 链接: https://redefine.ohevan.com/2023/09/20/第五章作业思路分享/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论