
第二章知识点总结

0 本章的核心问题
关联矩阵
(拓扑约束,反映各元件的连接方式)一般支路
(元件约束,主要是元件的伏安特性)大型网络的节点导纳矩阵如何生成
A阵、Bf阵、Qf阵的相互转化
1 关联矩阵
- 节点-支路关联矩阵
A - 基本回路-支路关联矩阵
Bf - 基本割集-支路关联矩阵
Qf
1.1 “有向回路”
对于一个电路而言,电流的方向是任意取定的;在电路图中,所取定的电流的方向就是该条支路的方向。
1.2 节点-支路关联矩阵 A阵
1.2.1 特点
- 行 对应 (除参考节点以外的)节点
- 列 对应
“有向”回路 - 元素
a只有01-1三种取值 - 若节点(含参考节点)共
m+1个、支路共n个,则A阵是m行n列的
1.2.2 如何生成A阵
为了生成A阵,只需:
- 遍历节点和支路
- 判断节点与支路是否直接连接的关系
- 支路流入节点,
a值取-1 - 支路流出节点,
a值取1 - 若该支路与该节点无上述关系,
a值取0。
- 支路流入节点,
1.2.3 举例
支路的方向如图给定所示,以节点1为例
- 支路
b1流出节点,故a = 1 - 支路
b5流入节点,故a = -1 - 支路
b4流入节点,故a = 1 - 其余支路与节点1不直接相连,故
a = 0
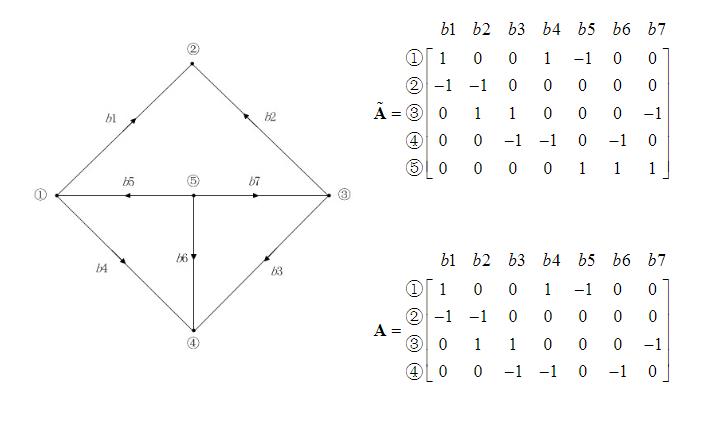
图中,较上位置的矩阵称为节点-支路关联矩阵的增广矩阵
1.3 基本回路-支路关联矩阵 Bf阵
1.3.1 树支和连支
树支所构成的支路集满足:
- 能将每个节点都连在一起
- 再添加一条支路,电路中就有闭合回路
连支就是 除了树枝以外的 其他支路
1.3.1 基本回路
- 一个
网孔就是一个基本回路 基本回路数等于连支数
1.3.2 Bf阵中元素的确定
- 由
连支方向确定基本回路的方向 - 遍历基本回路和支路确定
Bf中元素- 支路与
基本回路同向,则b = 1 - 支路与
基本回路反向,则b = -1 - 支路不在
基本回路内,则b = 0
- 支路与
1.3.3 举例
支路和基本回路的方向如图给定所示,以回路l1为例
- 支路
b1与基本回路l1,故b = -1 - 支路
b2与基本回路l1,故b = 1
…
- 支路
b7不在基本回路l1内,故b = 0
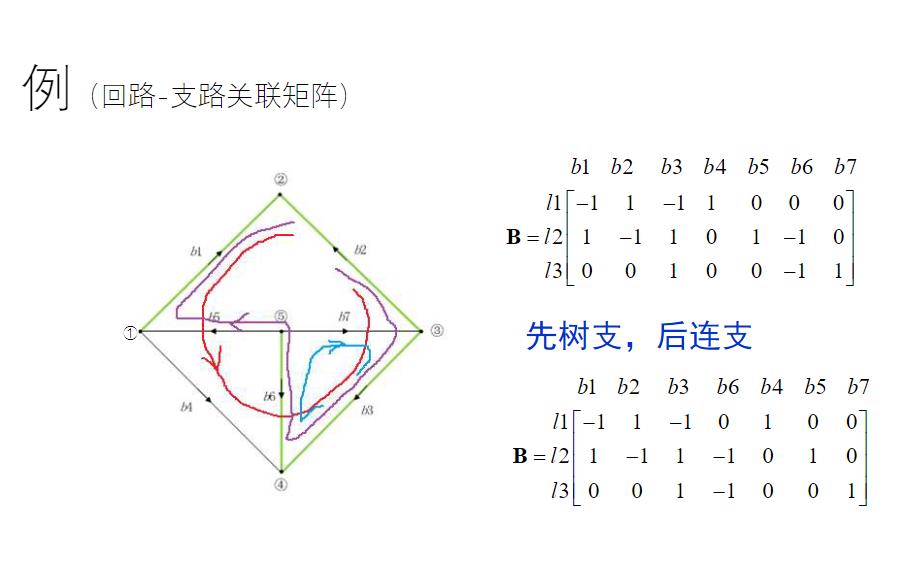
1.3.4 Bf阵的特点
将Bf阵中的列向量按照树支在前,连支在后的原则排列,则有:
基本回路与连支的矩阵是单位阵
1.4 基本割集-支路关联矩阵 Qf阵
1.4.1 基本割集
只切割一条树支,就能将一个图分成两个开放的图;这种切割方法能划分出基本割集。
1.4.2 支路相对割集的方向
把标记支路方向的箭头,全部挪到“割线”的一侧,再确定支路相对割集的方向。
1.4.3 Qf阵中元素的确定
- 若
支路与树支相对割集的方向相同,则b = 1 - 若
支路与树支相对割集的方向相反,则b = 1 - 若支路与割集无关,则
b = 0
1.4.4 举例
割集的分法、支路的方向如图给定所示,以割集为例
- 支路
b1与树支b1方向相同,故q = 1
…
- 支路
b4与树支b1方向相同,故q = 0
…
- 支路
b7与割集无关,故q = 0
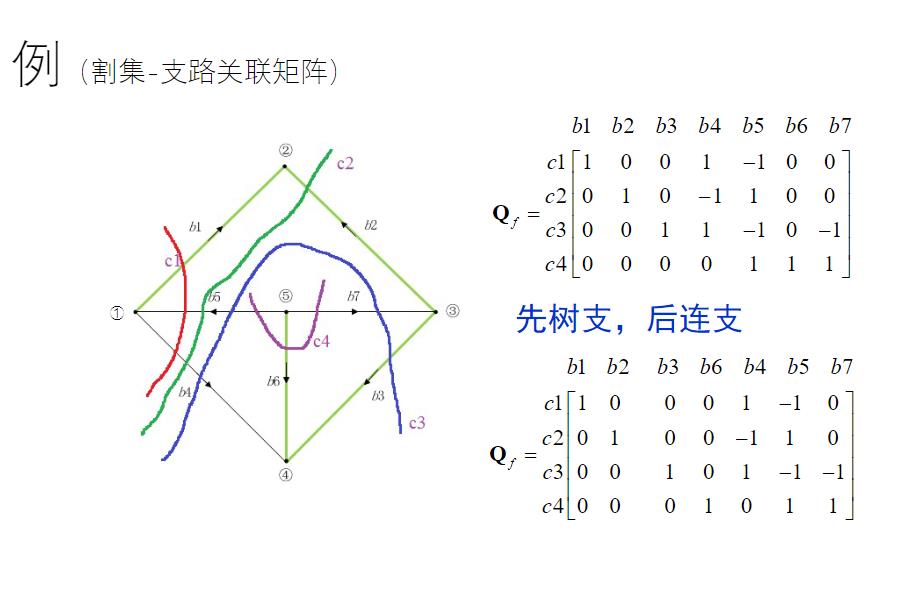
1.4.5 Qf阵的特点
将Qf阵中的列向量按照树支在前,连支在后的原则排列,则有:
割集与树支的矩阵是单位阵
2 一般支路
- 包含受控源的一般支路
- 不含受控源的一般支路
注:含受控源的一般支路,并不在本文讨论范围之内;若你有学习需求,可以上网或联系作者。
2.1 一般支路的拓扑
一般支路中,包含
- 阻抗
- 电流源
- 电压源
如图为一般支路各物理量的标号及正方向约定
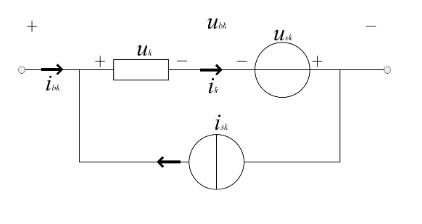
其中,阻抗的伏安特性起着:联系电压与电流两个不同物理量的重要作用。
2.2 一般支路的方程
根据伏安特性,列出一般支路的方程如下

这个方程是从单一支路推广到多个支路的。
- 从单一支路角度看,物理量的列向量“坍塌”成一个物理量;
- 从多个支路角度看,物理量的列向量是由一个一个一般支路组合在一起形成的。
3 上述理论的应用————生成大型网络的节点导纳矩阵Y阵
3.1 KCL和KVL的矩阵形式
3.1.1 KCL的矩阵形式
3.1.2 KVL的矩阵形式
3.2 用A阵和Yb阵生成节点导纳矩阵
- 标题: 第二章知识点总结
- 作者: JinYu
- 创建于 : 2023-09-19 18:48:10
- 更新于 : 2023-09-20 20:33:07
- 链接: https://redefine.ohevan.com/2023/09/19/《电网络》第二章知识点总结/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论